《数据结构与算法》第4章 队列(C语言)

BruceOu
目录 隐藏
4.1队列的概述
4.2顺序队列
4.2.1顺序队列概述
假溢出问题
4.2.2顺序队列实现
顺序队列存储结构实现
顺序队列的基本操作
4.3链式队列
4.3.1链式队列概述
4.3.2链式队列实现
链式队列存储结构实现
链式队列的基本操作
代码获取方法

4.1队列的概述

队列（queue）是一种先进先出（First In First Out , FIFO）的线性表，它只允许在表的一端插入元素，另一端删除元素。其中，允许插入的一端称为队尾（rear），允许删除的一端称为对头（front）。

和栈一样，也是一种对数据的"存"和"取"有严格要求的线性存储结构。

与栈结构不同的是，队列的两端都"开口"，要求数据只能从一端进，从另一端出，如图所示：

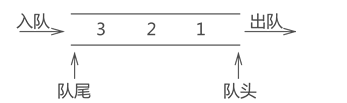
241mn0.png

通常，称进数据的一端为 "队尾"，出数据的一端为 "队头"，数据元素进队列的过程称为 "入队"，出队列的过程称为 "出队"。

不仅如此，队列中数据的进出要遵循 "先进先出" 的原则，即最先进队列的数据元素，同样要最先出队列。拿上图中的队列来说，从数据在队列中的存储状态可以分析出，元素 1 最先进队，其次是元素 2，最后是元素 3。此时如果将元素 3 出队，根据队列 "先进先出" 的特点，元素 1 要先出队列，元素 2 再出队列，最后才轮到元素 3 出队列。

栈和队列不要混淆，栈结构是一端封口，特点是"先进后出"；而队列的两端全是开口，特点是"先进先出"。
因此，数据从表的一端进，从另一端出，且遵循 "先进先出" 原则的线性存储结构就是队列。

队列存储结构的实现有以下两种方式：

  • 顺序队列：在顺序表的基础上实现的队列结构；
  • 链队列：在链表的基础上实现的队列结构；

两者的区别仅是顺序表和链表的区别，即在实际的物理空间中，数据集中存储的队列是顺序队列，分散存储的队列是链队列。

实际生活中，队列的应用随处可见，比如排队买 XXX、医院的挂号系统等，采用的都是队列的结构。

拿排队买票来说，所有的人排成一队，先到者排的就靠前，后到者只能从队尾排队等待，队中的每个人都必须等到自己前面的所有人全部买票成功并从队头出队后，才轮到自己买票。这就不是典型的队列结构吗？

4.2顺序队列

4.2.1顺序队列概述

顺序队列，即采用顺序表模拟实现的队列结构。

我们知道，队列具有以下两个特点：

  • 数据从队列的一端进，另一端出；
  • 数据的入队和出队遵循"先进先出"的原则；

因此，只要使用顺序表按以上两个要求操作数据，即可实现顺序队列。

顺序队列通常采用一维数组存储队列中的元素，另外增加两个指针分别指示数组中存放的队首元素和队尾元素。其中指向队首元素的指针称为队头指针front，指向队尾元素的指针称为队尾指针rear。

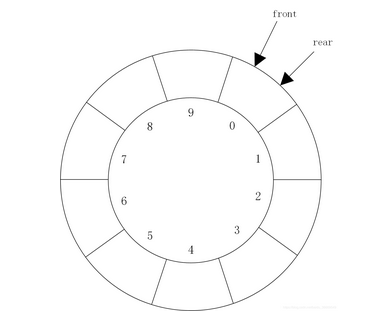
队列为空时，队头指针front和队尾指针rear都指向下标为0的存储单元，当元素a,b,c,d,e,f,g依次进入队列后，元素a~ g分别存放在数组下标为0~6的存储单元中，队头指针front指向元素a，队尾指针指rear向元素g的下一位置。如图所示。

241nBV.png

假溢出问题

顺序队列在前文的结构中，容易出现“假溢出”。所谓“假溢出”，就是经过多次插入和删除操作后，实际队列还有存储空间，但是又无法向队列中插入元素。

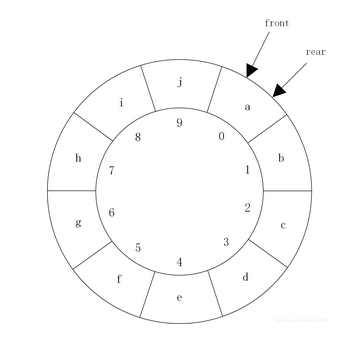
例如在图中队列删除a和b，然后依次插入h、i和j，当插入j后，就会出现队尾指针rear越出数组的下界造成“假溢出”，如图所示。

241u7T.md.png

当队尾指针rear或队头指针front到达存储空间的最大值时（假定队列的存储空间为SIZE），让队尾指针或者队头指针转化为0，这样就可以将元素插入到队列的空闲存储单元中，有效的利用存储空间，消除“假溢出”。
例如在上面的例子中，插入元素j后，rear将变为0，这样就将j插入下标为0的存储单元中。这样顺序队列的存储空间就构成了一个逻辑上收尾相连的循环队列。

要把用数组表示的顺序队列构成循环队列，只需要一个简单的取余操作即可实现。例如当队尾指针rear=9（假设SIZE=10）时，如果要将新元素入队，则先令rear=（rear+1）%10,这样rear就等于0，这样利用取余操作就实现了队列逻辑上的首尾相连，然后将元素存入队列的第0号单元。

4.2.2顺序队列实现

顺序队列存储结构实现

#define SIZE 10

typedef int data_t;

typedef struct _sequeue_t
{
    data_t data[SIZE];
    int front;
    int rear;
}sequeue_t;

【注】顺序队列也可以通过指针实现。

顺序队列的基本操作

(1)顺序队列的初始化

顺序队列初始化很简单，只需要将对头和对尾下表置为0即可。

sequeue_t *sequeue_create()
{
    sequeue_t *queue = (sequeue_t *)malloc(sizeof(sequeue_t));

    queue->front = 0;
    queue->rear = 0;

    return queue;
}

在循环队列中，队空和队满时队头front和队尾指针rear同时都会指向同一存储单元，即front==rear。

241MAU.png

(2)判断顺序队列是否为空

判断顺序队列是否为空只需要判断对头和对尾下标是否相等即可。

int sequeue_is_empty(sequeue_t *queue)
{
    if(queue == NULL)
        return -1;
    return ((queue->front == queue->rear)?1:0);
}

(3)判断顺序队列是否为满

判断顺序队列是否为满只需要判断对头和对尾下标差值是否为SIZE-1。

241QNF.png

int sequeue_is_full(sequeue_t *queue)
{
    if(queue == NULL)
    {
        return -1;
    }

    return ((queue->rear + 1) % SIZE == queue->front ? 1 : 0);  
}

如何区分队空和队满呢？有以下两种方法：

（1）增加一个标志位。设标志位为tag,初始时，tag=0;当入队成功，则tag=1；出队成功，tag=0。则判断队空的条件为：front \= = rear&&tag \= = 0;队满的条件为：front \= = rear&&tag \= = 1;

（2）少用一个存储单元。队空的判断条件为front \= = rear；队满的判断条件为front \= = (rear+1）%SIZE。
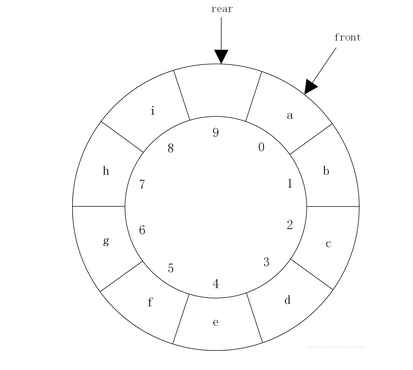
队满的状态如图。笔者使用的第二种。

241lh4.png

(4)判断顺序队列是否为空

int sequeue_is_empty(sequeue_t *queue)
{
    if(queue == NULL)
        return -1;
    return ((queue->front == queue->rear)?1:0);
}

(5)判断顺序队列是否为满

int sequeue_is_full(sequeue_t *queue)
{
    if(queue == NULL)
    {
        return -1;
    }

    return ((queue->rear + 1) % SIZE == queue->front ? 1 : 0);
}

(6)清空顺序队列

void sequeue_clear(sequeue_t *queue)
{
    if(queue != NULL)
        queue->rear = queue->front=0;
}

(7)顺序队列入队

int sequeue_en(sequeue_t *queue, data_t data)
{
    if (sequeue_is_full(queue))
    {
        printf("queue is full!\n");
        return -1;
    }
    queue->data[queue->rear] = data;
    queue->rear = (queue->rear + 1) % SIZE;

    return 0;
}

(8)顺序队列出队

data_t sequeue_de(sequeue_t *queue)
{
    if(queue ==NULL)
    {
        return -1;
    }
    if (sequeue_is_empty(queue))
    {
        printf("queue is empty!\n");
        return -1;
    }

    data_t data = queue->data[queue->front];
    queue->front = (queue->front + 1) % SIZE;

    return data;
}

(9)打印顺序队列

void sequeue_show(sequeue_t *queue)
{
    int i;
    for (i = queue->front; i < queue->rear; i++)
    {
        printf("%d, ", queue->data[i % SIZE]);
    }
    printf("\n");
}

(10)释放顺序队列

void sequeue_destroy(sequeue_t **queue)
{
    free(*queue);
    *queue = NULL;
}

4.3链式队列

4.3.1链式队列概述

链式队列，简称"链队列"，即使用链表实现的队列存储结构。

链式队列的实现思想同顺序队列类似，只需创建两个指针（命名为 front和 rear）分别指向链表中队列的队头元素和队尾元素，如图所示:。

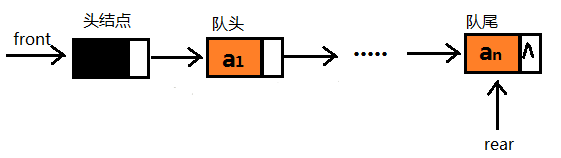
24139J.png

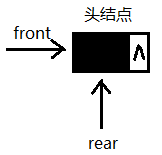
空队列时，front和rear都指向头结点。下图所示为链式队列的初始状态，此时队列中没有存储任何数据元素，因此 front和 rear 指针都同时指向头节点。和链表一样，为了防止表的丢失等问题，我们将留出一个标志节点，有时称为表头(header)或哑结点(dummy node)。因此只有在初始化时front和 rear 指针都同时指向头节点。

241839.png

4.3.2链式队列实现

链式队列存储结构实现

typedef int data_t;

typedef struct _qnode
{
    data_t data;
    struct _qnode *next;
} linkqnode_t, *linkqnode;

typedef struct
{
    linkqnode front, rear;
} linkqueue_t;

链式队列的基本操作

(1)链式队列的初始化

linkqueue_t *CreateEmptyLinkqueue()
{
    linkqueue_t *lqueue;

    lqueue = (linkqueue_t *)malloc(sizeof(linkqueue_t));
    if(lqueue == NULL)
        return NULL;

    lqueue->front = lqueue->rear = (linkqnode_t*)malloc(sizeof(linkqnode_t));

    if(lqueue->front == NULL)
        return NULL;

    lqueue->front->next = NULL;

    return lqueue;
}

(2)判断链式队列是否为空

int EmptyLinkqueue(linkqueue_t *lqueue)
{
    if(lqueue == NULL)
        return -1;

    return ((lqueue->front->next == lqueue->rear)?1:0);
}

(3)链式队列入队

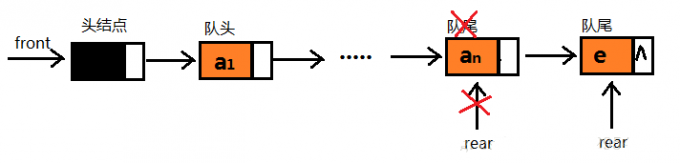
链队队列中，当有新的数据元素入队，只需进行以下 3 步操作：

  1. 将该数据元素用节点包裹，例如新节点名称为 p；
  2. 与 rear 指针指向的节点建立逻辑关系，即执行 lqueue->rear->next=p；
  3. 最后移动 rear 指针指向该新节点，即 lqueue->rear=p；

由此，新节点就入队成功了。

241GcR.md.png

int EnLinkqueue(linkqueue_t *lqueue, data_t x)
{
    linkqnode_t *p;
    if(lqueue == NULL)
        return -1;

    p = (linkqnode_t*)malloc(sizeof(linkqnode_t));
    if(p == NULL)
    {
        return -1;
    }
    p->data = x;
    p->next = NULL;

    if(lqueue->front->next == NULL)
    {
        lqueue->front->next = lqueue->rear = p;
    }
    else
    {
        lqueue->rear->next = p;
        lqueue->rear = p;
    }
    return 0;
}

(4)链式队列出队

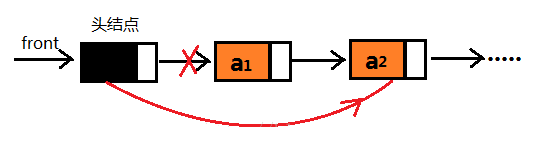
当链式队列中，有数据元素需要出队时，按照 "先进先出" 的原则，只需将存储该数据的节点以及它之前入队的元素节点按照原则依次出队即可。这里，我们先学习如何将队头元素出队。

  1. 通过 front指针直接找到队头节点，创建一个新指针node_remove 指向此即将出队的节点；
  2. 将 node_remove 节点（即要出队的队头节点）从链表中摘除；
  3. 释放节点 node_remove，回收其所占的内存空间；

241Jj1.png

int DeLinkqueue(linkqueue_t *lqueue,data_t *x)
{
    linkqnode_t *node_remove;
    if(lqueue == NULL || lqueue->front->next == NULL)
    {
        return -1;
    }
    node_remove = lqueue->front->next;
    lqueue->front->next = node_remove->next;

    if(x != NULL)
    {
        *x = node_remove->data;
    }
    free(node_remove);
    return 0;
}

(5)打印链式队列

void Linkqueue_show(linkqueue_t *lqueue)
{
    linkqnode_t *p;

    if(lqueue->front)
    {
        p = lqueue->front->next;
    }
    while(p)
    {
        printf("%d ",p->data);
        p = p->next;
    }
    printf("\n");
}

(6)清空链式队列

void ClearLinkqueue(linkqueue_t *lqueue)
{
    linkqnode_t *qnode;

    while(lqueue->front->next)
    {
        qnode = lqueue->front->next;
        lqueue->front->next= qnode->next;
        free(qnode);
    }
    lqueue->rear = NULL;
}

(7)释放链式队列

void DestroyLinkqueue(linkqueue_t *lqueue)
{
    if(lqueue != NULL)
    {
        if(EmptyLinkqueue(lqueue) != 1)
        {
            ClearLinkqueue(lqueue);
        }
        free(lqueue);
    }
}

代码获取方法

1.关注公众号[嵌入式实验楼]
2.在公众号回复关键词[Data Structures and Algorithms]获取资料

嵌入式实验楼

Related posts

Leave a Comment